Cube Root Calculator

The Cube Root Calculator is an essential tool for anyone needing to determine the cube root (or 3rd root) of a positive number. This versatile tool not only simplifies the process of finding cube roots but also allows users to cube numbers with ease. Whether you're solving mathematical problems, identifying perfect cubes, or calculating roots of other degrees, the Cube Root Calculator ensures accuracy and efficiency.

What is the Cube Root of a Number?

The cube root of a number x is a value y such that: ³√x = y ⟺ y³ = x

It can also be expressed in another mathematical form: ³√x = x^(1/3)

In simple terms, finding the cube root involves identifying a number that, when multiplied by itself three times, equals the original value. For instance, what is the cube root of 27? It is 3, because 3³ = 27. This concept is foundational in both basic arithmetic and advanced mathematical applications.

A Geometric Perspective on Cube Roots

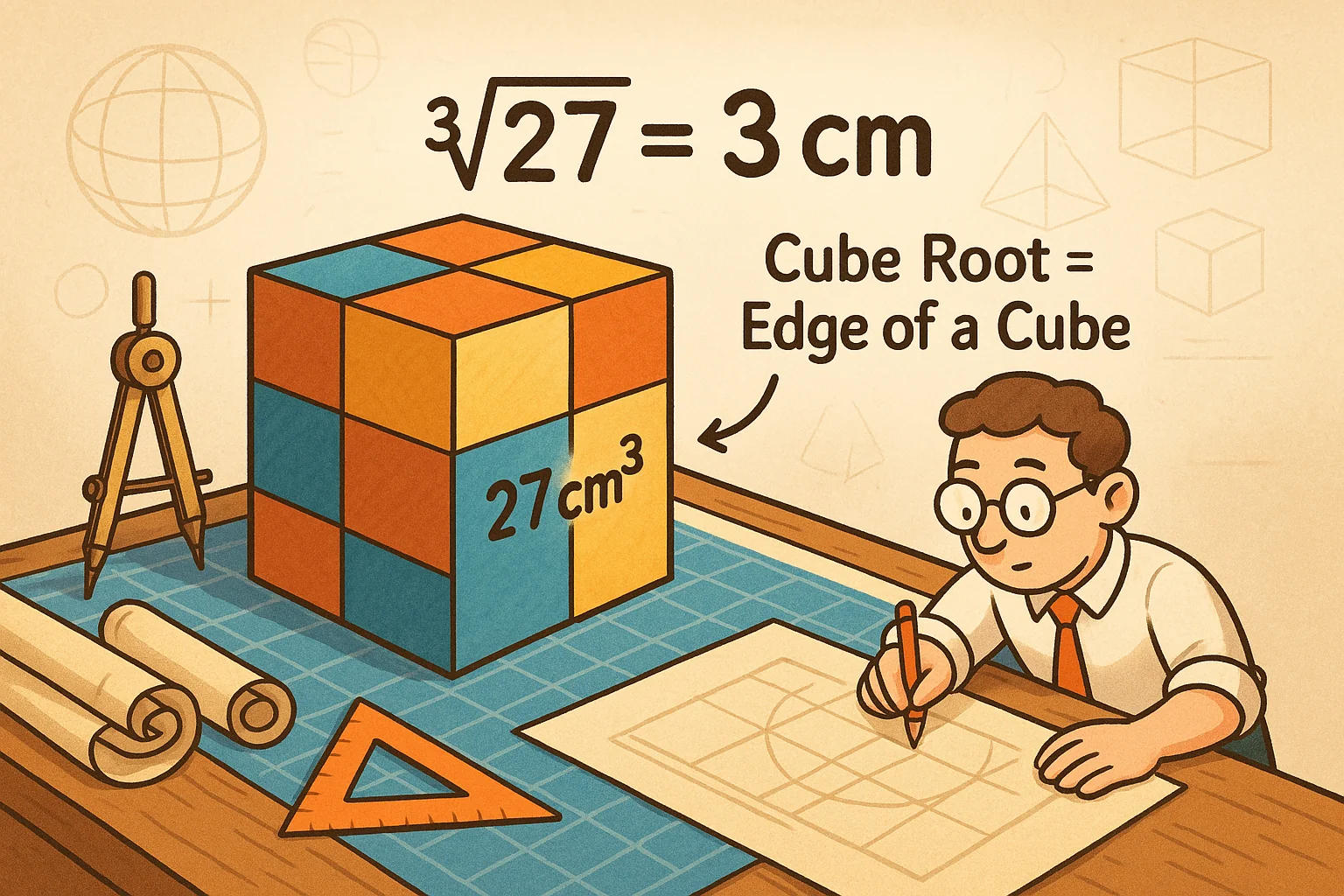
From a geometric standpoint, the cube root has a direct connection to three-dimensional shapes. Consider a cube with a volume of 27 cm³. To determine the length of one of its edges, you would calculate the cube root of its volume. In this case, the edge length would be 3 cm because 3³ = 27. This interpretation makes cube roots particularly useful in fields like architecture, engineering, and design, where spatial calculations are crucial.

Perfect Cubes

Perfect cubes are numbers that are the result of cubing whole numbers. Recognizing these values can simplify many mathematical operations. Here’s a list of some common perfect cubes:

These values are often used in geometry, physics, and mathematics for quick reference and problem-solving. Identifying perfect cubes is particularly helpful when working with cube root calculations or determining whether a given number can be expressed as the cube of an integer.

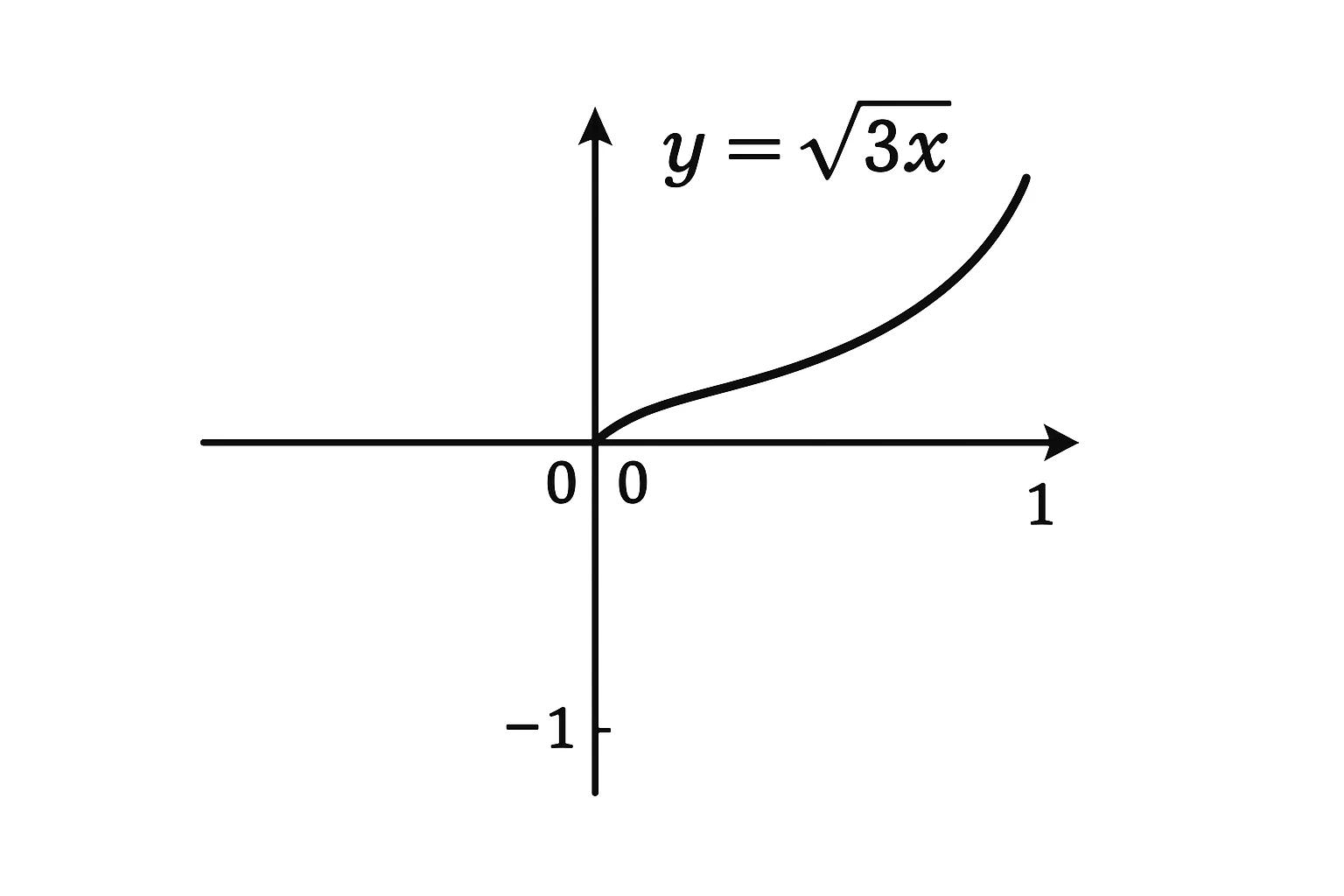
Cube Root Function and Graph

The cube root function, represented as ³√x = y, is an odd function, meaning it is symmetric with respect to the origin. This symmetry implies that:
f(−x) = −f(x), for all x.

Characteristics of the cube root function:

• Passes through the origin: The point (0, 0) is a natural intersection for the graph.
• Domain and Range: Both are all real numbers (ℝ).
• Behavior: As x approaches positive infinity, y also grows. Similarly, as x approaches negative infinity, y becomes smaller.

The graph of ³√x = y demonstrates a gentle curve, gradually increasing or decreasing. This smooth behavior makes it visually distinct from quadratic or square root functions, which have sharper changes in their graphs.

How to Use the Cube Root Calculator

Using the Cube Root Calculator is straightforward:

Step 1: Enter the positive number you want to find the cube root of.
Step 2: Click the “Calculate” button.
Step 3: View the result, which will be displayed instantly.

For additional functionality, you can use this third root calculator to find the cube of a number by entering your desired value and selecting the corresponding operation.