Square Root Calculator

If you're interested in calculations involving other types of roots, check out the General Roots Calculator - an advanced version that supports various root operations.

What is Square Root?

The square root is a fundamental mathematical operation that represents a number which, when multiplied by itself, yields the original value. For example, the square root of 25 is 5 because 5×5=25. The commonly used symbol for square root is √ , and the value under the radical sign is called the radicand.

Square Root Symbol

The symbol √  is widely used in mathematics to represent the square root operation. This radical symbol originates from the Latin letter "r," standing for radix (root), reflecting the fundamental idea of the operation: finding the base value that, when squared, equals the original number.

The square root symbol has been in use since the 16th century, first appearing in the work of mathematician Christoph Rudolff. Over centuries, this notation has become an indispensable part of modern mathematics, particularly in algebra, geometry, and calculus.

The square root notation has also been extended to represent more complex operations, such as cube roots (∛ ) or nth roots (𝑛√), which help solve a variety of mathematical problems. For instance, when working with polynomials or nonlinear equations, this symbol simplifies and clearly expresses mathematical expressions.

Square Root of Negative Numbers

The square root of a negative number does not exist within the real number system because no real number, when squared, equals a negative value. However, in the complex number system, the square root of a negative number is expressed as i√|x| , where i is the imaginary unit defined by the property i^2= - 1. For example:

√-9 = 3i 

Operations of Square Root

Operations involving square roots follow specific rules that govern addition, subtraction, multiplication, and division. These rules ensure that calculations remain consistent, even when working with irrational numbers. Let’s explore each operation in detail:

• Addition and Subtraction

Square roots cannot be directly added or subtracted unless their radicands (the values under the square root) are the same. This is because the square root operation does not distribute over addition or subtraction.

For instance: √9 + √16 = 3 + 4 = 7

In this example, the square roots are calculated separately before being added together. However, for expressions like √9 + √8, simplification is not possible because the radicands differ.

In some cases, simplifying radicands might reveal common factors. For example:

√50 + √18 = √25×2 + √9×2 = 5√2 + 3√2 = 8√2

• Multiplication

Square roots can be multiplied by combining their radicands under a single square root, following the property:

√a ×√b = √ab

• Division

Similarly, square roots can be divided by combining their radicands under a single square root, following the rule:

√a /√b=√(a/b)

When dividing, it is important to ensure the denominator does not include a square root. If it does, rationalizing the denominator is necessary. For example:

Derivative of the Square Root

In calculus, the derivative of the square root function, √x is derived using the rules of differentiation for power functions. Expressing √x as x^1/2we apply the power rule:

This formula reveals that the rate of change of √𝑥 decreases as 𝑥 increases, reflecting the gradual flattening of its curve.

Example:

Let f(x)=√x. To find the derivative at x = 4:

This means the slope of the tangent to the graph of y=√x at x = 4 is 0.25

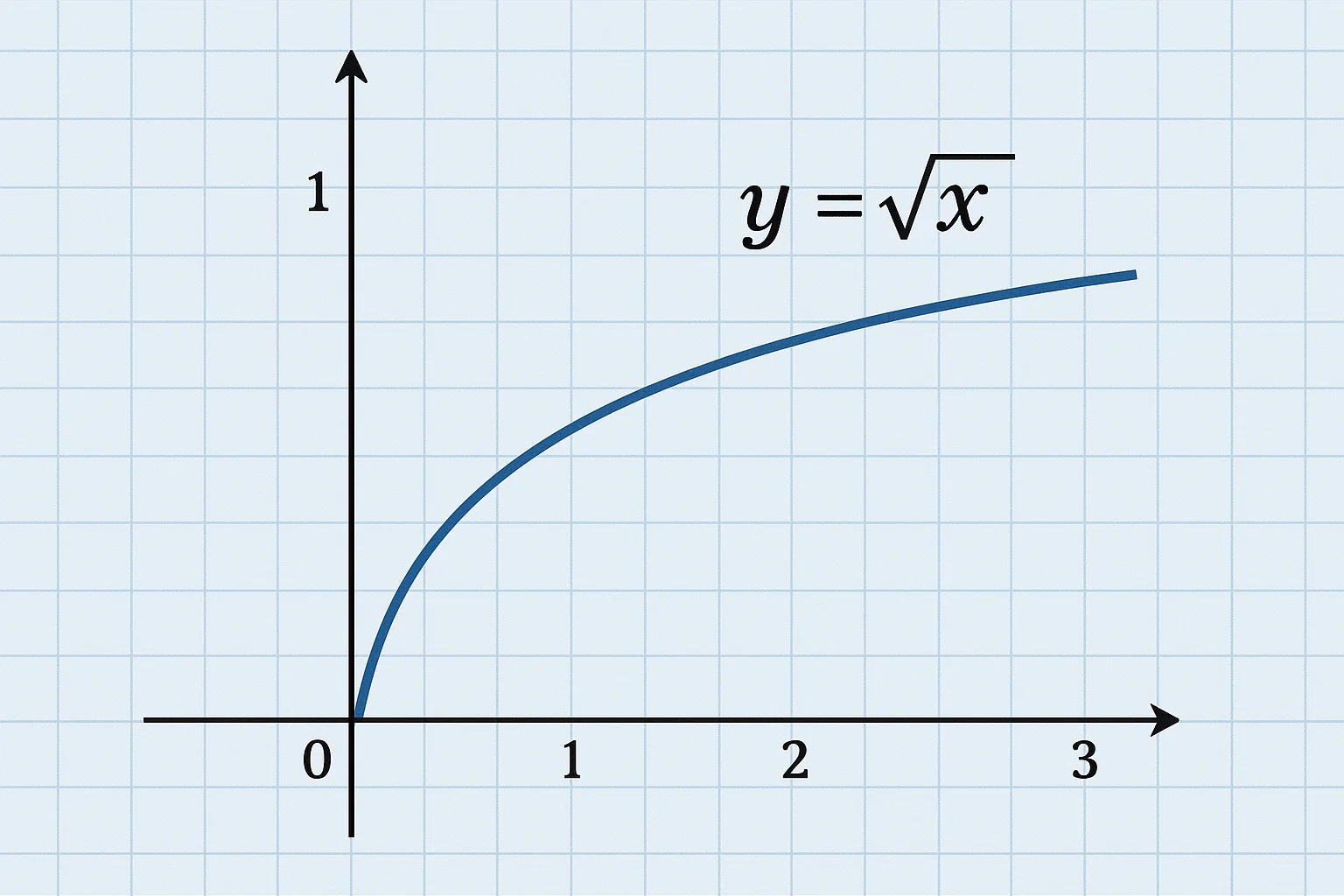
Graph of the Square Root

The graph of the square root function, y=√x as a distinct shape resembling half of a parabola lying above the x-axis. It starts at the origin 

(0,0) and only exists when x0 in the real number set, as square roots of negative numbers are undefined in real numbers.

Square Root of Powers and Fractions

Square roots extend naturally to both powers and fractions, following specific mathematical properties:

• Square Root of Powers: The square root of xn can be expressed as: xn =xn/2
• Square Root of Fractions: The square root of a fraction is calculated by taking the square root of both the numerator and the denominator: