Temperature conversion is a crucial aspect of various scientific, industrial, and everyday applications. Whether you're adjusting a recipe, conducting a chemistry experiment, or dealing with international weather reports, knowing how to convert between temperature units is essential. Some conversions, like Celsius to Kelvin, are relatively simple, while others, like Celsius to Fahrenheit, require more complex calculations. Fortunately, temperature conversion tools like a temp conversion calculator exist to make the process effortless, eliminating the need to memorize formulas.
Beyond practical conversions, temperature itself is a fascinating concept. It is not just a number on a thermometer but a fundamental property of matter, directly tied to the movement of atoms and molecules. Understanding temperature in both everyday and scientific contexts provides deeper insights into how heat and energy interact in our world.
What is Temperature?
While temperature seems like a straightforward concept—often understood as how hot or cold something is—it is much more complex when examined scientifically.
The Challenge of Defining Temperature
Defining temperature in everyday terms is surprisingly difficult. Most people think of temperature in relation to human perception—whether something feels warm, cold, or just right. However, this subjective experience does not provide a precise measurement.
Temperature is not just about sensation; it is a fundamental property of matter that determines the state and behavior of substances. A temperature calculator or thermometer provides a numerical value for temperature, but what does that number actually represent?
Scientific Explanation of Temperature
At a microscopic level, temperature is directly related to the movement of atoms and molecules. In scientific terms, temperature is a measure of the average kinetic energy of particles within a substance. The faster these particles move, the higher the temperature.
For example:
- High temperatures: Atoms and molecules move rapidly.
- Low temperatures: Particles move more slowly.
- Absolute zero (0K or -273.15°C): Theoretical point where all molecular motion stops.
This explains why temperature affects the state of matter. When a solid is heated, its particles move faster until they break free, turning into a liquid. If heating continues, the particles gain even more energy and transition into a gas.
Connection to Thermal Energy
Temperature is closely related to heat, which is a form of kinetic energy. While temperature measures how fast particles are moving, heat refers to the total energy transferred due to a temperature difference.
For instance:
- When you touch a hot surface, heat flows from the object to your skin.
- When you hold an ice cube, heat from your hand moves into the ice, causing it to melt.
Temperature and Other Physical Properties
Temperature is not an isolated physical property—it directly influences various other properties of matter, including pressure, volume, and density. These interconnections are particularly important in physics, chemistry, and engineering, where understanding how temperature interacts with other factors helps explain everything from weather patterns to industrial processes.
Interconnectedness of Temperature, Pressure, Volume, and Density
In gases, temperature plays a crucial role in determining both pressure and volume. When the temperature of a gas increases, its particles move faster and collide with the walls of their container more frequently and with greater force, leading to an increase in pressure if the volume remains constant. Conversely, if the gas is allowed to expand, the volume increases to accommodate the heightened energy levels while maintaining constant pressure.
Density, which is the mass per unit volume of a substance, is also affected by temperature. In most materials, higher temperatures lead to lower density because heating causes expansion, increasing volume while keeping mass constant. This principle explains why hot air rises—warmer air is less dense than the cooler air around it, leading to convection currents that play a fundamental role in atmospheric dynamics.

The Ideal Gas Law
The Ideal Gas Law mathematically expresses the relationship between temperature, pressure, and volume in a gas:
PV = nRT
Where:
P = Pressure
V = Volume
n = Number of moles of gas
R = Universal gas constant
T = Temperature (in Kelvin)
This equation illustrates that temperature and pressure are directly proportional when volume is constant. It also explains why, for example, a car tire's pressure increases on a hot day—the added heat raises the temperature of the air inside, increasing its pressure.
Specific Properties
Beyond pressure and volume, temperature influences three critical thermal properties of materials:
- Specific Heat Capacity: The amount of heat required to raise the temperature of one unit mass of a substance by one degree. Water, for example, has a high specific heat, meaning it takes a lot of energy to change its temperature, which is why oceans regulate climate.
- Latent Heat: The heat required for a phase change (e.g., solid to liquid, liquid to gas) without changing temperature. This explains why ice at 0°C does not immediately become water at 1°C—it needs latent heat to overcome the molecular bonds keeping it solid.
- Thermal Conductivity: The ability of a material to transfer heat. Metals, like copper and aluminum, have high thermal conductivity, which is why they are used in cookware and heat exchangers. Insulating materials like wool or Styrofoam have low thermal conductivity, making them ideal for heat retention.
Temperature Scales
Temperature is measured using different scales and units, each with unique historical and scientific significance. While Celsius, Fahrenheit, and Kelvin are the most widely used, several lesser-known scales have been developed throughout history.
Common Temperature Scales
- Celsius (°C) – The metric system’s standard scale, based on water's freezing (0°C) and boiling points (100°C).
- Fahrenheit (°F) – Used mainly in the U.S., this scale sets water’s freezing point at 32°F and boiling at 212°F.
- Kelvin (K) – The absolute temperature scale used in scientific calculations, starting at absolute zero (0K = -273.15°C).
- Rankine (°R) – A lesser-known scale used in thermodynamics, similar to Kelvin but based on the Fahrenheit system.
- Delisle (°D) – An inverted scale where higher temperatures have lower values, historically used in Russia.
- Newton (°N) – A rarely used scale devised by Isaac Newton for experimental heat measurements.
- Réaumur (°Ré) – Used in 18th-century Europe, particularly in France, before being replaced by Celsius.
- Rømer (°Rø) – Created by Danish astronomer Ole Rømer, this scale was an early predecessor to modern systems.
One of the biggest challenges in measuring temperature has been creating a universally accepted scale. Early temperature scales were inconsistent, often based on arbitrary reference points. Even today, different fields and regions use different units, causing temp conversion challenges.
The Kelvin scale helped resolve this issue by introducing an absolute reference point (absolute zero), making it the standard in scientific research. However, practical applications still rely on Celsius and Fahrenheit, leading to the continued need for temperature conversion between systems. A reliable temperature conversion calculator simplifies this process, eliminating manual effort and ensuring precision across scales.
Temperature Measurement Techniques
Measuring temperature has evolved significantly over time, from simple thermal expansion methods to advanced electrical and optical techniques used in scientific and industrial applications. Each method is suited for different environments, from measuring body temperature to determining the heat of distant stars.
Thermal Expansion
One of the earliest and most widely recognized temperature measurement methods is thermal expansion, which relies on the fact that substances expand when heated and contract when cooled.
Traditional liquid-in-glass thermometers use mercury or alcohol contained in a narrow glass tube. As temperature changes, the liquid expands or contracts, moving up or down a graduated scale.
- Mercury thermometers are highly accurate and were historically used in medical, industrial, and meteorological applications. However, due to mercury’s toxicity, they have been largely phased out.
- Alcohol thermometers are safer and can measure lower temperatures than mercury because alcohol remains liquid at much colder temperatures. They are often dyed for better visibility.
This method is still used today in basic thermometers but has largely been replaced by more advanced digital technologies, especially when paired with a temp conversion calculator for immediate temperature conversion across units.
Electrical Properties
Modern temperature measurement techniques use electrical properties to provide more accurate, rapid, and automated readings. Two of the most common methods are electrical resistance thermometers (RTDs) and thermocouples.
Resistance Temperature Detectors (RTDs)
RTDs measure temperature by taking advantage of how a material's electrical resistance changes with temperature. The most common RTDs use platinum, as its resistance increases in a predictable manner with temperature.
- Advantages: High accuracy, stable readings, and suitable for a wide range of temperatures.
- Common Applications: Industrial processes, scientific laboratories, and meteorology.
Thermocouples
A thermocouple consists of two different metal wires joined at one end. When the junction experiences a temperature difference, it produces a voltage that correlates to temperature, based on the Seebeck effect.
- Advantages: Fast response time, durability, and ability to withstand extreme temperatures.
- Common Applications: Used in industrial furnaces, automotive sensors, and aerospace engineering.
Thermocouples are widely used due to their ruggedness and ability to measure a vast range of temperatures, from cryogenic levels to thousands of degrees Celsius. These sensors, when integrated with a temperature calculator or temperature conversion calculator, provide valuable data for real-time applications across diverse industries.
Color and Light Measurement
In environments where direct contact is impossible—such as measuring the temperature of stars, molten metals, or high-temperature reactors—scientists rely on color and light measurement techniques.
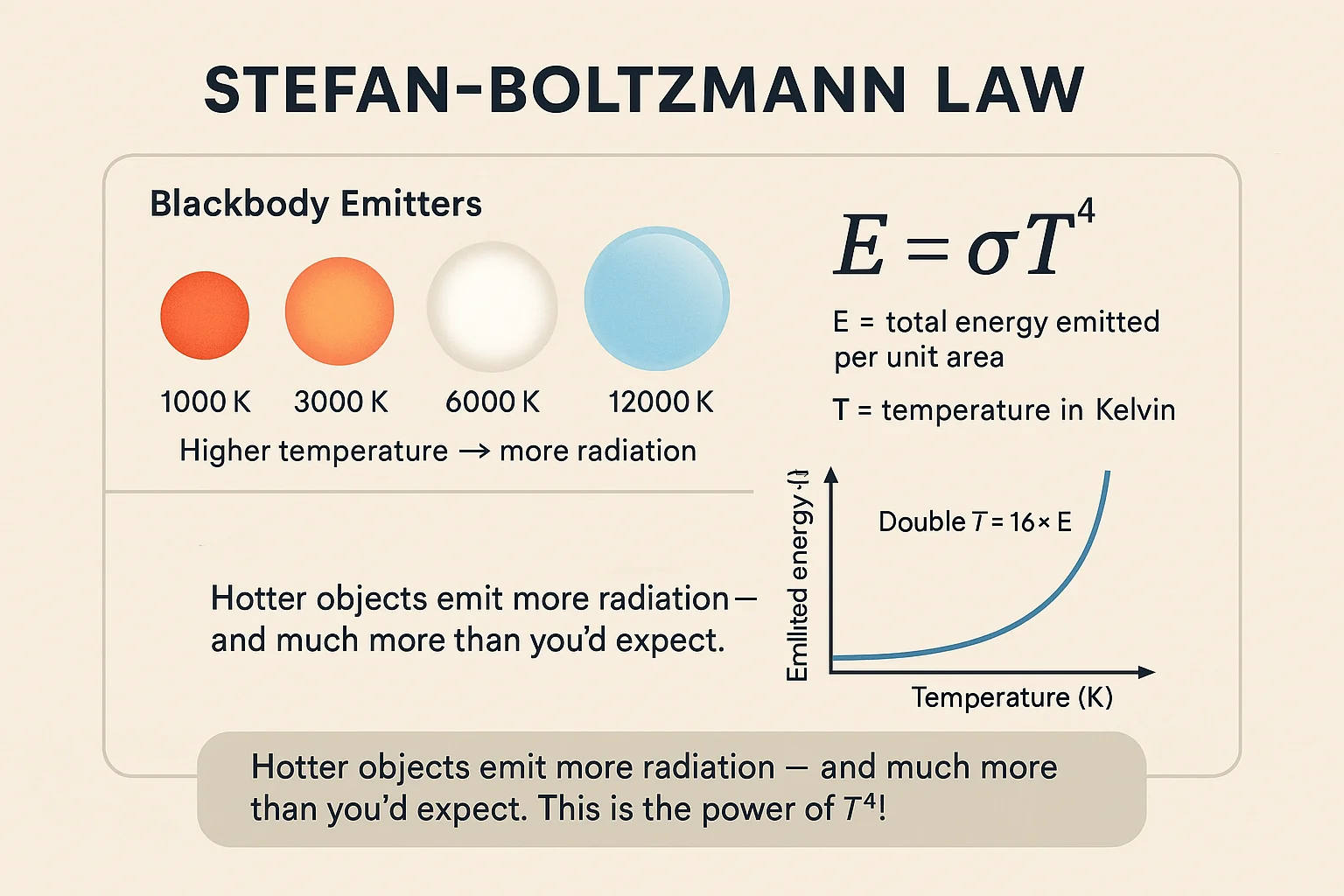
Stefan-Boltzmann Law
The Stefan-Boltzmann law states that the total energy radiated by an object is proportional to the fourth power of its absolute temperature:
E = T⁴
Where E is the emitted energy, T is the absolute temperature in Kelvin, and σ is the Stefan-Boltzmann constant.
This principle allows astronomers to estimate the temperatures of stars by measuring their total energy output.
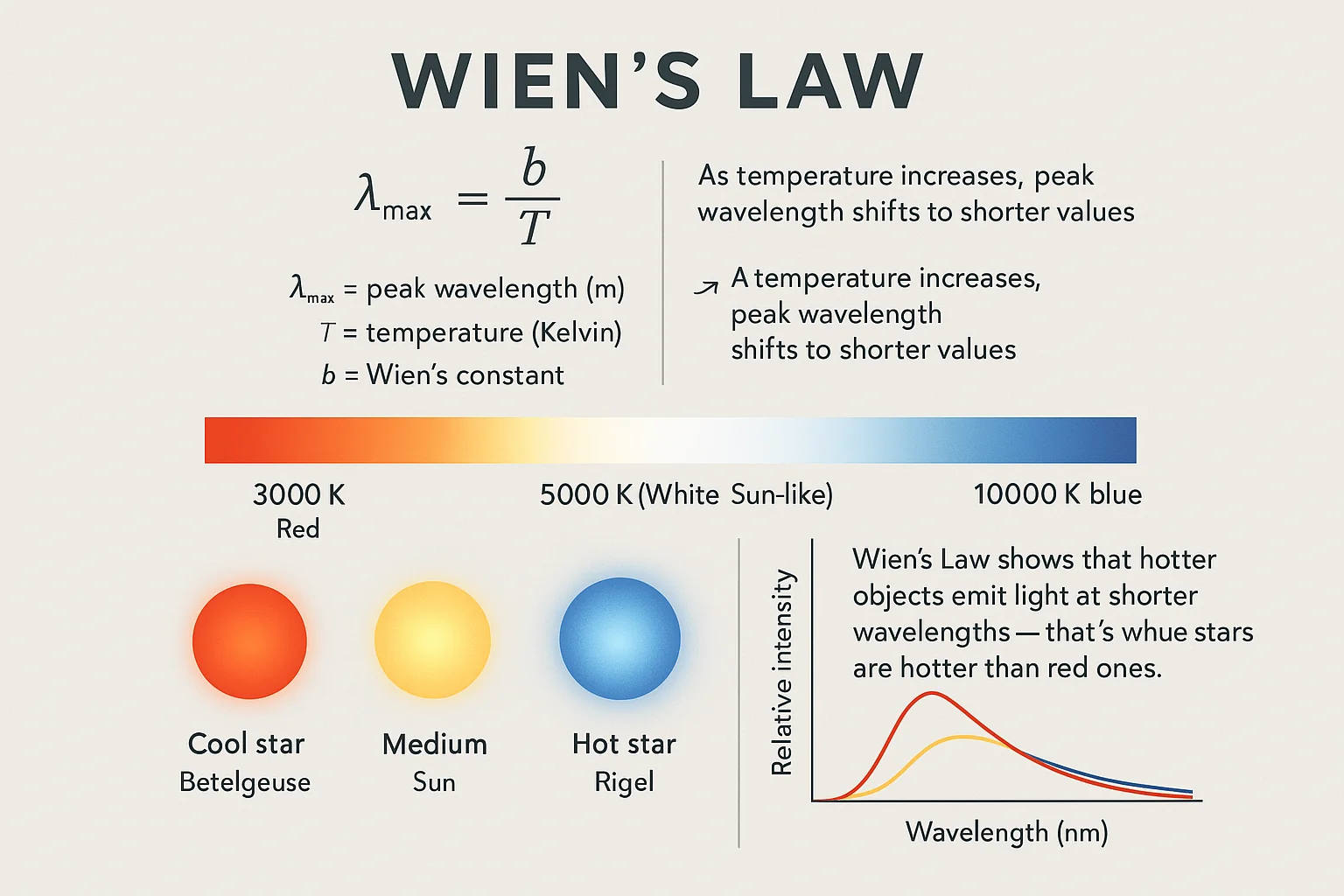
Wien’s Law
Wien’s displacement law relates the peak wavelength of emitted radiation to an object's temperature:
λmax = b / T
Where λmax is the wavelength of maximum emission, b is Wien’s constant, and T is temperature in Kelvin.
This law explains why hotter stars appear blue and cooler stars appear red. By analyzing the light spectrum of a star, scientists can accurately determine its temperature. For terrestrial applications, this principle is foundational in advanced optical sensors and supports temp conversion accuracy when combined with a temperature conversion tool.